

We have grown leaps and bounds to be the best Online Tuition Website in India with immensely talented Vedantu Master Teachers, from the most reputed institutions. Vedantu LIVE Online Master Classes is an incredibly personalized tutoring platform for you, while you are staying at your home. Here, Coulombs come in handy for measuring the charges held by household electrical circuits. In a house, ordinarily, we use a 100-watt power lightbulb that draws out 1 ampere of current. This is the sole reason why Physicists use a huge unit like Columb for lump sump of electrons flowing through a wire. So, in 1 C, the number of electrons flowing through the above copper wire is 6.25 x 10¹⁸. On Solving, we get the value of 1 Coulomb charge as 6.25 x 10¹⁸. Now, if the charge is 1 C, then the number of electrons will be = 1/1.6 x 10⁻¹⁹ C When the charge is 1.6 x 10⁻¹⁹ C, the number of electrons = 1 Let’s say an electrical circuit carries a charge of the magnitude 1.6 x 10⁻¹⁹ C. The ‘q’ is a charge of 1 C, the formula is:įor the number of electrons, we re-write the equation in the following way: So, if there are ‘n’ number of electrons flowing through a wire where ‘e’ is an elementary charge of the magnitude, i.e., 1.6 x 10⁻¹⁹ C. So, we could clearly define one Coulomb from the above statement.Īccording to the law of conservation of charges, whatever electrons flow through the wire, are quantized and also they remain conserved. When the current of 1 ampere flows through this wire, 1 Coulomb of electrons, i.e., 6.25 x 10¹⁸ electrons pass through it every second, i.e., given by: Now, why do Physicist use such a big unit for a charge? Well! Its understanding is easy by going more in mathematics beyond it. Let’s suppose that there are millions of charges flowing through a copper wire in the following manner: Let’s understand the Coulomb SI unit in detail: So, from the above statement of 1 Coulomb, we understood that the value of 1 Coulomb charge is equal to 6.25 x 10¹⁸ or 6.24 quintillion electrons. This quantity was named Coulomb in the 18th–19th-century after a French physicist named Charles-Augustin de Coulomb, one Coulomb is approximately equal to 6.25 × 10 18 electrons. We define Coulomb as the quantity of electricity transported in one second by a current of one ampere. In an International Systems, the unit of electric charge is the meter-kilogram-second-ampere, which is the basis of the SI system of physical units. On solving, we get the value of k = 8.99 x 10⁹Nm☬⁻² Here, k is the proportionality constant called the Columb’s law Constant, and its value is calculated in the following manner:įrom the above equation, we can re-arrange to determine the value of k: So, in both cases, the equation remains the same for the force and that is:Īs the force remains proportional to the product of charges and the square of the distance between these, so, on removing the sign of proportionality constant, we generate the following new form of the above equation: If there were charges of the same magnitude, also the same polarities, then there would have an electrostatic force of repulsion between them because these charges are static and are joined together with an imaginary line. So, when these charges apply forces on each other, they generate a force, which is the electrostatic force of attraction, as the charges are of the same magnitude but with different polarities. The distance between the two charges remains constant. The unit was so named as an honour to Mr Coulomb in 1880 after the discovery of Coulomb’s law by him in 1785.Īccording to Coulomb’s law, if two charges are separated by a distance ‘r’, and the charges are of opposite polarities as well. In International Systems or SI systems, the unit of an electric charge is Coulom.

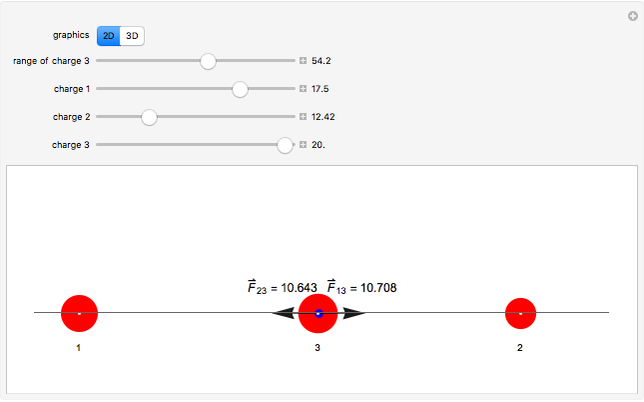
A French Military Engineer and Physicist named Charles-Augustin de Coulomb brought the concept of electrostatic forces (attractive and repulsive) between two charges placed inline apart with a square of the distance that lies inversely proportional to this force however, the product of two charges always remains directly proportional to this force.


 0 kommentar(er)
0 kommentar(er)
